We consider whether for COVID-19, 1.1r^2.5 provides a good estimate for Ro, the number of people one person may infect when there is no natural immunity.
We have already established that r^2.5 provides a good estimate for the effective reproduction rate Re, where r is the daily increase in case numbers. We want to estimate Ro.
We eventually consider the following table.
The formula at the top of our table is our original estimate for Ro (actually an estimate for Re). For simplicity we call this f.
Originally we used n =10 (since there are 10 days when a person is infectious).
Since we have already discovered that r^2.5 provides a good estimate for Re, we now compare this value for re with the value obtained using the formula when n = 2.5.
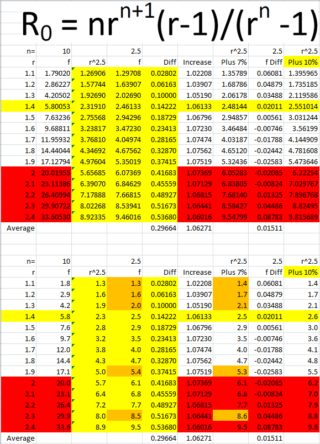
The bottom half of the table contains values in the top half rounded to one decimal place.
The last column is our estimate for Ro = 1.1r^2.5
We look at New Zealand data early in the original 2020 outbreak.
We see that r = 1.4 fits the New Zealand case numbers well early in 2020.

From the first table we read that for r = 1.4, Ro = 2.6.
One person may on average infect 2.6 others over a 10-day infectious period.
Firstly we look at this table:
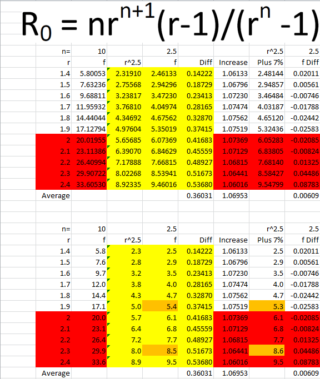
We see that on average the formula gives a result that is 7% above the value obtained for r^2.5.
Note that the values highlighted in red would not be obtained in practice.
Instead of 7%, we add on 10% to estimate Ro and obtain our original table (see last column):

You may find the PDF easier to read:
COVIDformula2023
We see that the values for f when n = 2.5 lie between r^2.5 and 1.1r^2.5.
We use this to obtain a range for Ro.
For r = 1.4 (highlighted in yellow) we estimate Ro to be in the range from 2.3 to 2.6.
We use values in the last column (the higher number in our range) as our estimate for Ro.
We conclude that 1.1r^2.5 is a good estimate for Ro.
We note that when r = 1.4 (as in NZ) r^2 =1.96.
This suggests that case numbers may almost double each two days.
This suggests that r = SQRT(2) may provide a good estimate for Ro.
Note that SQRT(2) ~ 1.414214
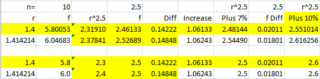
We conclude that 1.1r^2.5 is a good estimate for Ro.