My Christmas gift to you: my main site is now publicly available again:
https://aaamazingphoenix.wordpress.com/
All links on Altervista should now work.

My Christmas gift to you: my main site is now publicly available again:
https://aaamazingphoenix.wordpress.com/
All links on Altervista should now work.

We se the results in our previous post to calculate worldwide estimates for Ro in 2020 using data up to mid-August 2020.
We obtain the following table:
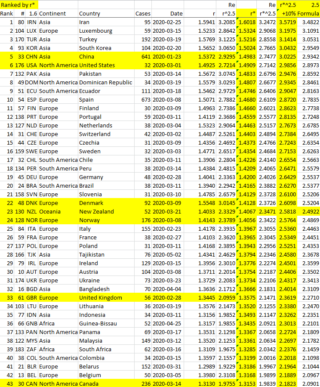
For more countries see:
COVIDWorldAllCasesCPMNZcorr
Notes:
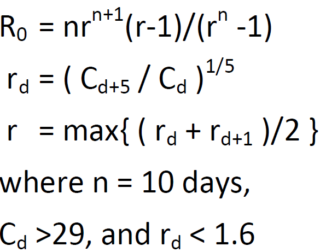
Historically we used n = 10 in the formula on the first line above. Most recently we use n = 2.5.
We note that in New Zealand r = 1.4033 and r* = 1.4067, both very close to 1.4 estimated in our previous post:
We consider whether for COVID-19, 1.1r^2.5 provides a good estimate for Ro, the number of people one person may infect when there is no natural immunity.
We have already established that r^2.5 provides a good estimate for the effective reproduction rate Re, where r is the daily increase in case numbers. We want to estimate Ro.
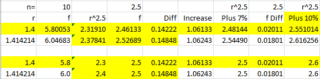
We eventually consider the following table.
The formula at the top of our table is our original estimate for Ro (actually an estimate for Re). For simplicity we call this f.
Originally we used n =10 (since there are 10 days when a person is infectious).
Since we have already discovered that r^2.5 provides a good estimate for Re, we now compare this value for re with the value obtained using the formula when n = 2.5.
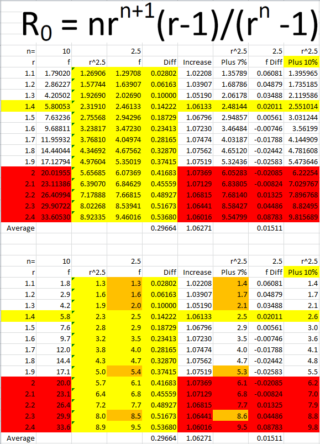
The bottom half of the table contains values in the top half rounded to one decimal place.
The last column is our estimate for Ro = 1.1r^2.5
We look at New Zealand data early in the original 2020 outbreak.
We see that r = 1.4 fits the New Zealand case numbers well early in 2020.

From the first table we read that for r = 1.4, Ro = 2.6.
One person may on average infect 2.6 others over a 10-day infectious period.
Firstly we look at this table:
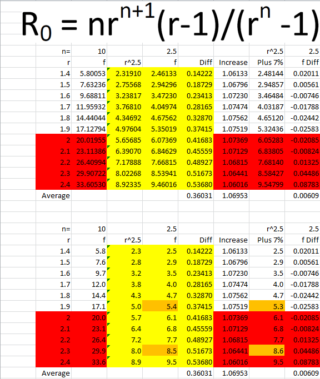
We see that on average the formula gives a result that is 7% above the value obtained for r^2.5.
Note that the values highlighted in red would not be obtained in practice.
Instead of 7%, we add on 10% to estimate Ro and obtain our original table (see last column):

You may find the PDF easier to read:
COVIDformula2023
We see that the values for f when n = 2.5 lie between r^2.5 and 1.1r^2.5.
We use this to obtain a range for Ro.
For r = 1.4 (highlighted in yellow) we estimate Ro to be in the range from 2.3 to 2.6.
We use values in the last column (the higher number in our range) as our estimate for Ro.
We conclude that 1.1r^2.5 is a good estimate for Ro.
We note that when r = 1.4 (as in NZ) r^2 =1.96.
This suggests that case numbers may almost double each two days.
This suggests that r = SQRT(2) may provide a good estimate for Ro.
Note that SQRT(2) ~ 1.414214
We conclude that 1.1r^2.5 is a good estimate for Ro.

COVID Odyssey Addendum
Summer has ceased Autumn’s awesome
My thoughts come least my mind’s caught numb
I feel like an April fool
I have sealed my time capsule
Before adding my addendum
Alan Grace
26 March 2022
The COVID Odyssey website has become an open Time Capsule:
Alan Grace: COVID Odyssey Time Capsule for aaamazingphoenix.wordpress.com – Warning: Most Links within posts will go to the original site: aaamazingphoenix.wordpress.com
A version of this post can be found here:
COVID Odyssey: Autumn Addendum Post #971~ COVID Odyssey Time Capsule Addendum – COVID Odyssey: Alan Grace’s vir[tu]al journey (wordpress.com)

This addendum covers:
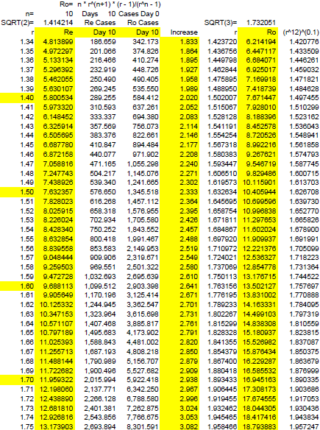
This PDF may be easier to read and contains a wider range of values:
CasesReRoC5
The actual value for Ro will lie between our values calculated for Re and Ro.
We could also estimate Ro using r^1.1, the geometric mean of r and r^1.2. We obtain:
CasesReRoD
In the first 2020 Outbreak New Zealand, r =1.4 and hence r^2 = 1.96. This is close to 2 so we thought that when r = 1.4, for Ro, r was close to SQRT(2). At a minimum this could be the case. Let z = ln( SQRT(2) ) / ln(1.4) and use r^z in our formula where z = 1.030021359. This gives the result we require when r = 1.4. We obtain (see image below):
CasesReRoE
CasesReRoE2
(the last two columns show the increase in r when estimating Ro)
CasesReRoE3
(includes Ro/Re)
This provides low estimates for Ro, close to Re as required when r = 1.4. We adopt these estimates.

Both Re and Ro are estimated using this formula:
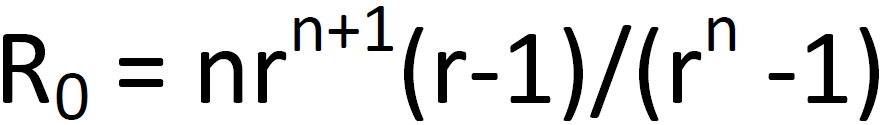
where n = 10 Days.
For our upper estimate in the range for Ro, substitute r^1.2 for r in the formula.
Please see the WELCOME menu for background and definitions at:
COVID Odyssey: Alan Grace’s vir[tu]al journey – COVID Odyssey: Alan Grace’s vir[tu]al journey investigating/experiencing COVID-19 life (wordpress.com)

My COVID-19 posts can be found in the COVID-19 menu or here:
https://aaamazingphoenix.wordpress.com/tag/coronavirus/
(Alan’s Ark contains old posts from the above site)
Data for my posts can be found at:
https://www.worldometers.info/coronavirus/
https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_New_Zealand
I share my posts at:
https://guestdailyposts.wordpress.com/guest-pingbacks/
Create a website and earn with Altervista - Disclaimer - Report Abuse